곡률반지름은 곡선의 극히 짧은 구간을 원호로 환산할 때 그 원호의 반지름을 곡률반지름이라고 합니다. 따라서 원의 곡률반지름은 그 원의 반지름이 되며 원 위의 모든 점에서 곡률반지름은 같습니다.
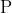 라하고 인접한 점을
라하고 인접한 점을 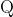 라하고
라하고 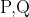 의 법선이 서로 만나는 점은
의 법선이 서로 만나는 점은 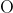 가 되고 점
가 되고 점 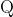 가 점
가 점 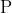 에 한없이 가까울 때 점
에 한없이 가까울 때 점 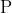 에 대한 곡률반지름은
에 대한 곡률반지름은 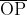 가 됩니다. 이를 수식으로 표현하면 아래와 같습니다.
가 됩니다. 이를 수식으로 표현하면 아래와 같습니다.
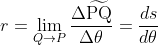 위 식을 통해 원에 대한 곡률반지름을 구하면, 먼저 짧은 구간의
위 식을 통해 원에 대한 곡률반지름을 구하면, 먼저 짧은 구간의 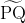 길이로 원을 100 등분해서 구하면
길이로 원을 100 등분해서 구하면 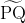 길이는 원둘레를 100으로 나눈 값이 되며 각도는 360을 100으로 나눈 값이 됩니다. 수식은 아래와 같습니다.
길이는 원둘레를 100으로 나눈 값이 되며 각도는 360을 100으로 나눈 값이 됩니다. 수식은 아래와 같습니다.
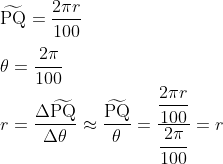 위의 값을 통해서 원의 곡률반지름은 그 원의 반지름이 됨을 알 수 있습니다.
위의 값을 통해서 원의 곡률반지름은 그 원의 반지름이 됨을 알 수 있습니다.
곡률은 곡률반지름의 역수이며 곡선의 휘어진 정도를 수치로 나타낼 때 곡률을 사용합니다.
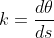 위는 곡률반지름의 역수인 곡률 수식입니다.
위는 곡률반지름의 역수인 곡률 수식입니다.
\\x=g\left ( t \right )\end{Bmatrix})
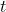 를 매개 변수로 하는 곡선의 수식이 위와 같이 주어지면, 아래와 같이 곡률 수식을 변경하여 곡률을 구합니다.
를 매개 변수로 하는 곡선의 수식이 위와 같이 주어지면, 아래와 같이 곡률 수식을 변경하여 곡률을 구합니다.
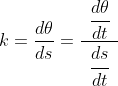 위 수식에서 미소 길이(위 그림에서
위 수식에서 미소 길이(위 그림에서 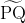 )에 대해 먼저 살펴보면, 위쪽 그림의
)에 대해 먼저 살펴보면, 위쪽 그림의 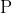 점에 대한 미소 곡선은 접선(위 그림에서
점에 대한 미소 곡선은 접선(위 그림에서 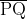 간 직선 길이)이며 접선 길이는 피타고라스 정리에 의해 아래와 같습니다.
간 직선 길이)이며 접선 길이는 피타고라스 정리에 의해 아래와 같습니다.
 \right )^2+\left ( \frac{d}{dx}y(t) \right )^2}=\sqrt{ {x'}^2+{y'}^2})
다음으로 미소 각(위 그림에서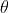 각)에 대해 살펴보면,
각)에 대해 살펴보면,
}{\frac{d}{dt}x(t)}=\frac{y'}{x'}) 위식은 미소각
위식은 미소각 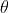 에 대한
에 대한 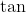 원리를 적용해 구한 식입니다.
원리를 적용해 구한 식입니다.
) 위식은
위식은 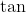 를
를 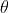 에 대해 먼저 미분한 식입니다.
에 대해 먼저 미분한 식입니다.
=\frac{y''x'-y'x''}{{x'}^2}\: \: \: \: \: \left (\because \left ( \frac{f(x)}{g(x)} \right )'=\frac{f'(x)g(x)-f(x)g'(x)}{{g^2(x)}} \right )) 위식은 몫의 미분법을 적용해 구한 식입니다.
위식은 몫의 미분법을 적용해 구한 식입니다.
위 식을 미소 각에 대해 정리를 하면 아래와 같습니다.
\\&=\frac{1}{1+\frac{{y'}^2}{{x'}^2}}\frac{y''x'-y'x''}{{x'}^2}=\frac{y''x'-y'x''}{{x'}^2+{y'}^2}\end{align*})
위 식들에서 곡률을 구하면 아래와 같습니다.
=\dfrac{\cfrac{d\theta }{dt}}{\cfrac{ds}{dt}}=\dfrac{\dfrac{y''x'-y'x''}{{x'}^2+{y'}^2}}{\sqrt{ {x'}^2+{y'}^2}})
=\frac{y''x'-y'x''}{\left ( {x'}^2+{y'}^2 \right )^\frac{3}{2}})
매개 변수를 이용하지 않는 수식의 곡률은 아래와 같습니다.
=\frac{f''(x)}{\left ( \left ( f'(x) \right )^2+1 \right )^{\frac{3}{2}}}\: \: \: \left ( \because x=t,\: \: \: x'=1,\: \: \: x''=0 \right ))
예제1) 포물선 곡률 구하기
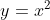
위 수식에 대한 곡률반지름과 곡률을 구하기 위해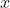 를
를 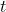 로 치환하여 구하면 아래와 같습니다.
로 치환하여 구하면 아래와 같습니다.
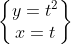
^{\frac{3}{2}}}{y''x'-y'x''}=\frac{\left ( 1^2+\left ( 2t \right )^2 \right )^{\frac{3}{2}}}{2\cdot 1-2t\cdot 0}=\frac{\left ( 4t^2+1 \right )^{\frac{3}{2}}}{2}=\frac{\left ( 4t^2+1 \right )\sqrt{4t^2+1}}{2}\\\\k=\frac{2}{\left ( 4t^2+1 \right )\sqrt{4t^2+1}}=\frac{2}{\left ( 4x^2+1 \right )\sqrt{4x^2+1}}\: \: \: \left ( \because x=t \right ))
위 수식을 그래프로 나타내면 아래와 같습니다.
예제2) 인벌류트 곡선의 곡률반지름
곡률은 곡률반지름의 역수이며 곡선의 휘어진 정도를 수치로 나타낼 때 곡률을 사용합니다.
다음으로 미소 각(위 그림에서
위 식을 미소 각에 대해 정리를 하면 아래와 같습니다.
위 식들에서 곡률을 구하면 아래와 같습니다.
매개 변수를 이용하지 않는 수식의 곡률은 아래와 같습니다.
예제1) 포물선 곡률 구하기
위 수식에 대한 곡률반지름과 곡률을 구하기 위해
위 수식을 그래프로 나타내면 아래와 같습니다.
예제2) 인벌류트 곡선의 곡률반지름

