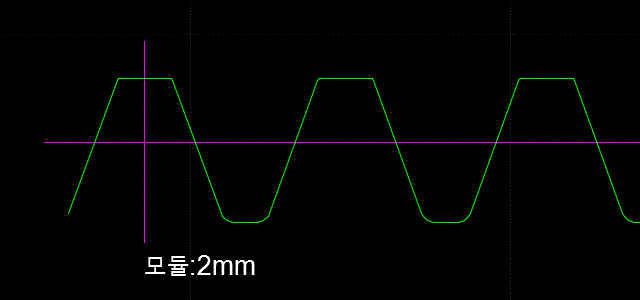
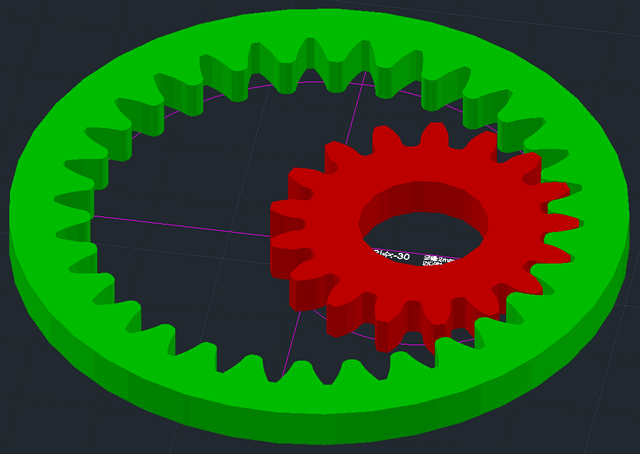
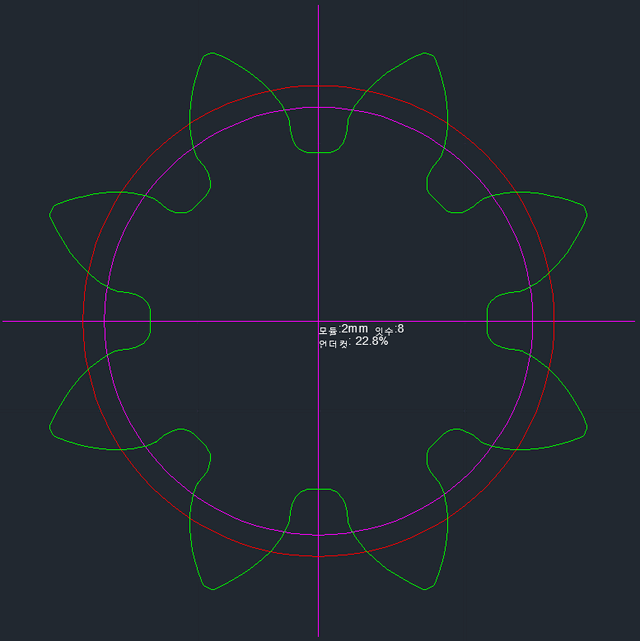
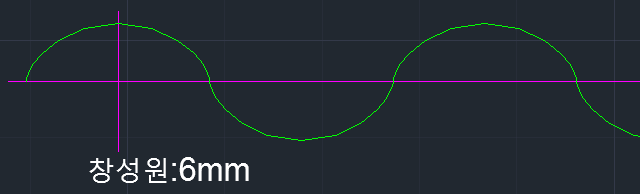
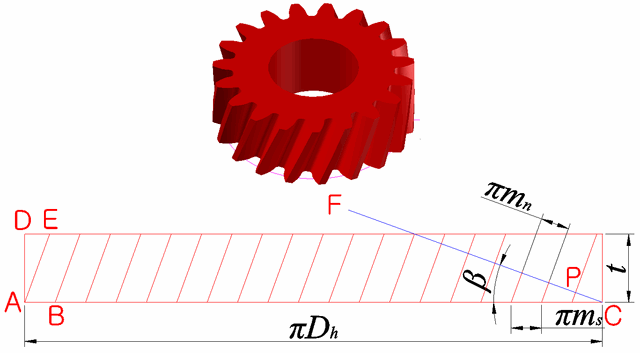
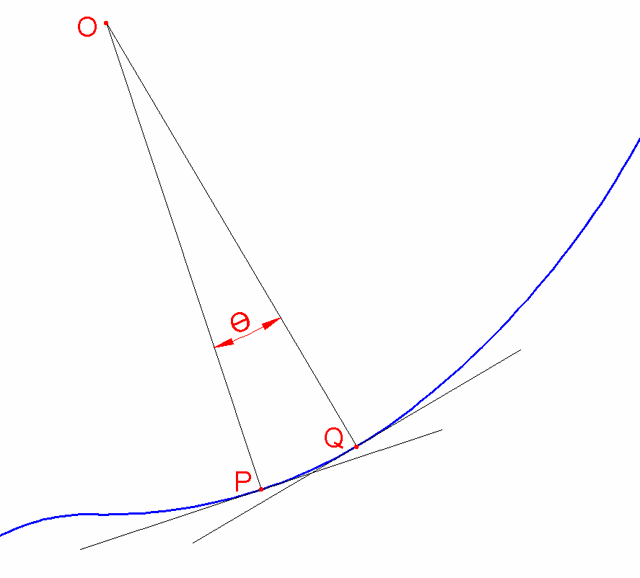
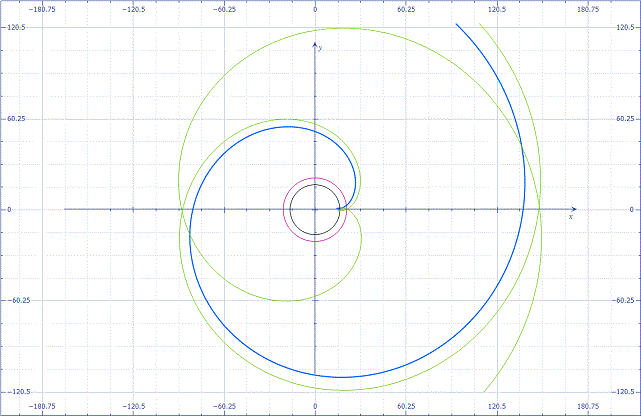
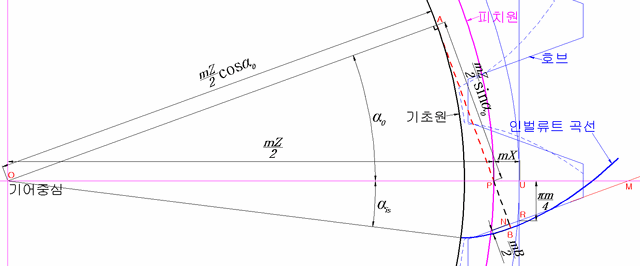
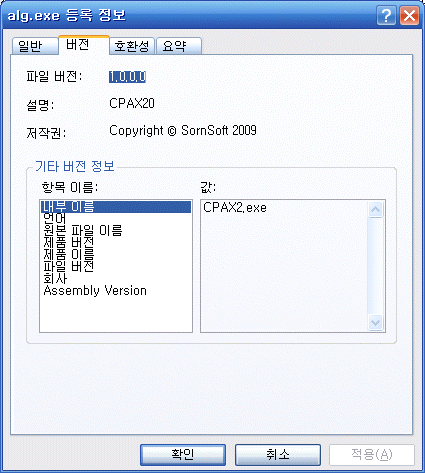
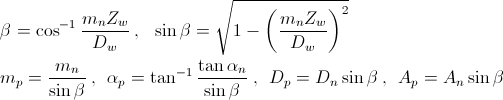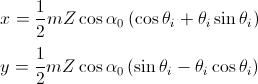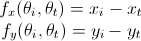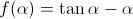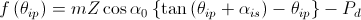인벌류트 치형을 형성하는 압력각, 전위, 백래쉬 등의 값들의 변화에 따라 기어 모양이 어떻게 변하는지를 지오지브라 프로그램을 통해 한눈에 확인할 수 있습니다. 지오지브라 웹사이트에서 바로 확인 할 수 있습니다. https://www.geogebra.org/m/npbtaauu 또는 지오지브라 프로그램을 설치하고 위의 "Involute_Gear,ggd"파일을 받아 열어 볼 수 있습니다. 기어 수식은 https://tro.kr/29 에 있으며 https://tro.kr/67 에 있는 LISP로 AutoCAD나 CADian에서 작도할 수 있습니다.