많은 문서에서 ' 는 무리수다'를 귀류법으로 증명하고 있는데 문제가 있습니다.
는 무리수다'를 귀류법으로 증명하고 있는데 문제가 있습니다.
 는 유리수가 아니다. =
는 유리수가 아니다. =  는 무리수이다.
위의 두 문장을 같다고 생각하여 귀류법으로 증명하는 듯합니다. 하지만 위 문장은 같지 않습니다. '유리수가 아니다'는 무리수나 허수일 수 있기 때문입니다.
는 무리수이다.
위의 두 문장을 같다고 생각하여 귀류법으로 증명하는 듯합니다. 하지만 위 문장은 같지 않습니다. '유리수가 아니다'는 무리수나 허수일 수 있기 때문입니다.
' 는 무리수이다'를 귀류법으로 증명하기 위해서는 '허수가 아니다'나 '
는 무리수이다'를 귀류법으로 증명하기 위해서는 '허수가 아니다'나 ' 는 실수다'를 먼저 증명해야 합니다.
는 실수다'를 먼저 증명해야 합니다.
수학은 '같음'만을 추구하는 학문이며 증명에서 다음 단계로 넘어가기 위해서는 반드시 '같음'이 인증되어야 합니다. 수학은 단 하나의 오류만 있어도 전체 증명을 부정합니다.
귀류법
귀류법(歸謬法)과 같은 말로 쓰이는 말은 배리법(背理法), 반증법(反證法)이 있습니다.
기본적으로 귀류법은 부정명제를 증명할 때 사용합니다. 즉, '~아니다'로 된 명제를 증명하는 방법입니다.
귀류법은 부정명제 문장을 긍정문장으로 바꾸고 긍정문장에 오류가 있음을 보여 부정명제가 참임을 증명하는 방법입니다. 귀류법의 장점은 긍정문장에서 단 하나의 오류만 찾으면 긍정문장 전체를 부정할 수 있습니다.
' 는 유리수가 아니다'증명하기 전에...
는 유리수가 아니다'증명하기 전에...
' 는 유리수가 아니다'긍정문으로 바꾸면 '
는 유리수가 아니다'긍정문으로 바꾸면 ' 는 유리수다'가 되며
는 유리수다'가 되며  가 무엇이며 유리수가 무엇인지 명확히 알아야합니다.
가 무엇이며 유리수가 무엇인지 명확히 알아야합니다.
유리수란?
분수로 나타낼 수 있는 수중에 분자는 정수, 분모는 자연수로 나타낼 수 있는 수로 아래와 같습니다.

유리수가 아닌 수
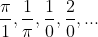
서로소란?
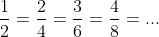
 을 위와 같이 여러 방법으로 쓸 수 있으며 분모와 분자가 더는 약분되지 않을 때 분모와 분자는 서로소이며 모든 유리수는 서로소인 분모와 분자로 나타낼 수 있습니다.
을 위와 같이 여러 방법으로 쓸 수 있으며 분모와 분자가 더는 약분되지 않을 때 분모와 분자는 서로소이며 모든 유리수는 서로소인 분모와 분자로 나타낼 수 있습니다.
분자와 분모가 서로소인 유리수는 아래와 같습니다.
제곱근이란?
 는 어떤 수를 2번 곱해서
는 어떤 수를 2번 곱해서  가 되는 어떤 수입니다. 예를 들어
가 되는 어떤 수입니다. 예를 들어 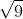 는 어떤 수를 2번 곱해서
는 어떤 수를 2번 곱해서 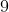 가 되는 어떤 수입니다. 즉, 어떤 수는
가 되는 어떤 수입니다. 즉, 어떤 수는 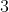 입니다.
입니다.
[증명] 는 유리수가 아니다.
는 유리수가 아니다.
이 내용은 BC 300년경에 활약한 그리스의 수학자 유클리드가 기록한 증명입니다.
1. 가 유리수라고 가정합니다.
가 유리수라고 가정합니다.
따라서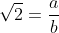 로 둘 수 있습니다. (
로 둘 수 있습니다. (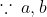 는 서로소입니다.)
는 서로소입니다.)
2. 양변에 를 곱하고 제곱하면
를 곱하고 제곱하면 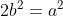 입니다. 어떤 수에
입니다. 어떤 수에  를 곱하면 짝수이므로
를 곱하면 짝수이므로  또한, 짝수입니다. 따라서
또한, 짝수입니다. 따라서  로 둘 수 있습니다.
로 둘 수 있습니다.
 를 치환하고 양변을
를 치환하고 양변을  로 나누면
로 나누면 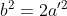 이므로
이므로  또한, 짝수입니다.
또한, 짝수입니다.
3.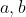 가 짝수이고
가 짝수이고  로 나누어지므로 서로소로 나타낼 수 없습니다. 이런 유리수는 존재하지 않으며 '
로 나누어지므로 서로소로 나타낼 수 없습니다. 이런 유리수는 존재하지 않으며 ' 가 유리수다'는 거짓입니다.
가 유리수다'는 거짓입니다.
'
수학은 '같음'만을 추구하는 학문이며 증명에서 다음 단계로 넘어가기 위해서는 반드시 '같음'이 인증되어야 합니다. 수학은 단 하나의 오류만 있어도 전체 증명을 부정합니다.
귀류법
귀류법(歸謬法)과 같은 말로 쓰이는 말은 배리법(背理法), 반증법(反證法)이 있습니다.
기본적으로 귀류법은 부정명제를 증명할 때 사용합니다. 즉, '~아니다'로 된 명제를 증명하는 방법입니다.
귀류법은 부정명제 문장을 긍정문장으로 바꾸고 긍정문장에 오류가 있음을 보여 부정명제가 참임을 증명하는 방법입니다. 귀류법의 장점은 긍정문장에서 단 하나의 오류만 찾으면 긍정문장 전체를 부정할 수 있습니다.
'
'
유리수란?
분수로 나타낼 수 있는 수중에 분자는 정수, 분모는 자연수로 나타낼 수 있는 수로 아래와 같습니다.
유리수가 아닌 수
서로소란?
분자와 분모가 서로소인 유리수는 아래와 같습니다.
제곱근이란?
[증명]
이 내용은 BC 300년경에 활약한 그리스의 수학자 유클리드가 기록한 증명입니다.
1.
따라서
2. 양변에
3.