위 그림은 모듈 2mm 치형을 0.5mm 단위로 전위를 하여 그린 기어들을 한곳에 겹친 그림입니다. (위 그림은 전위거리 값이며 전위계수에 모듈 값을 곱하면 전위거리가 됩니다.)
전위 값이 클수록 치형의 뿌리부분이 두껍고 치형의 끝부분은 얇아지는 것을 볼 수 있습니다.
위 그림의 좌측 위쪽 인벌류트(Involute) 곡선 부분은 모든 전위기어와 정확하게 겹쳐집니다. 단지 인벌류트(Involute) 곡선의 사용 범위가 다를 뿐입니다. 이는 일반기어를 사용함에 있어 축간 거리가 약간 달라져도 구동할 수 있음을 나타냅니다. 이는 인벌류트(Involute) 치형의 좋은 장점입니다.

위 그림은 전위기어와 일반기어가 물려 있는 그림입니다.
전위기어 이므로 전위 된 거리만큼 피치원이 서로 떨어져 있습니다.
접촉선은 전위기어의 기초원의 접선과 일반기어의 기초원의 접선으로 연결된 직선입니다. 위 그림처럼 전위기어와 일반기어가 물리면 백래시(backlash)가 발생합니다.(위 그림에서 전위 기어가 정회전하다가 역회전을 하면 백래시만큼 회전한 뒤에 일반기어로 동력 전달이 됩니다.) 일반기어의 피치원이 커지면 백래시 값은 작아집니다. 즉, 잇수가 많아지면 백래시값은 작아지며 랙과 물릴 때는 백래시가 없게 됩니다.
아래는 백래시 값을 구하는 수식을 유도하는 과정입니다.
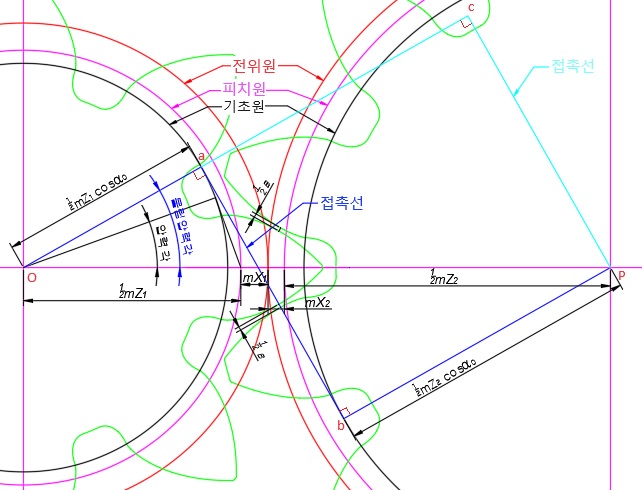
위 그림은 전위기어와 전위기어가 서로 물려 있는 그림입니다.(백래시는 아래와 위에 2군데 있습니다)
선분 bP와 선분 ac가 같고 선분 ab와 선분 Pc가 같습니다. 직각삼각형 OPc에서 물림압력각과 접촉선의 총길이를 구할 수 있습니다.

접촉선의 총길이에서 인벌류트 곡선까지의 거리를 빼면 백래시 거리를 구할 수 있습니다. 인벌류트 곡선까지의 거리는 아래 그림처럼 Z2를 랙기어로 치환해서 구 할 수 있습니다.

삼각형 Ose에서 se선분의 길이를 구하고 삼각형 efh에서 ef선분의 길이를 구해서 더하면 선분 sf의 길이가 됩니다. 물림압력각에 압력각을 뺀 값에서 기초원 반지름을 곱한 값에 선분 sf 길이를 더하면 선분 an의 길이가 됩니다.(전위기어가 s에서 a로 회전한 것이며 인벌류트 곡선의 정의에 의해 선분 sf의 길이가 선분 an이 되며 회전한 만큼 길어진 것입니다)
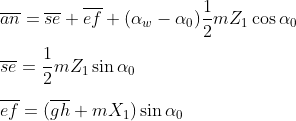
위와 같이 Z1을 랙기어로 치환해서 구하면


위 수식들을 정리하면



m: 모듈, Z1, Z2: 잇수, X1, X2: 전위계수, αw: 물림 압력각, α0: 압력각, lB: 백래시 거리, ls: 기어 중심간 거리
위 수식에서 백래시가 0이 되는 기어 중심거리를 구할 수 있습니다. 즉, 좌변이 0이 되는 ls 를 구할 수 있습니다. 이 ls 로 백래시가 없을 때 물림압력각(αw)을 구할 수 있습니다.

전위 기어를 일반 기어 값으로 환산을 해서 그려 보면 위 그림과 같이 인벌류트 곡선 부분이 정확히 일치하고 있으며 단지 백래시가 있는 기어임을 알 수 있습니다.

mt: 일반기어 모듈, m: 전위기어 모듈, Z: 잇수, X: 전위계수, αt: 일반기어 압력각, α0: 전위기어 압력각
위 식으로 전위기어를 일반기어값으로 바꿀 수 있습니다. 즉, 압력각과 모듈이 다른 기어가 서로 물려서 회전할 수 있음을 보이고 있습니다. 위의 식과 같은 규칙은 있지만 인벌류트 기어의 뛰어난 호환성을 보이고 있습니다.(모듈 2mm 압력각 20도 전위계수 0.95 잇수 19 기어와 모듈 2.2mm 압력각 31.3212579296513도 백래시 0.106495527mm 전위계수 0 잇수 12 기어와 같은 인벌류트 곡선임을 보이고 있습니다.)
