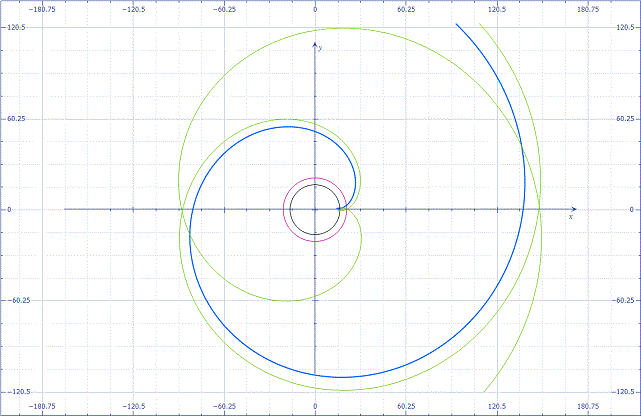
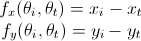인벌류트 기어의 치형 작도를 위한 수치해석에서 언더컷이 발생하면 θis, θte를 다시 구해야 완전한 치형을 작도 할 수 있습니다. 위는 인벌류트 곡선의 수식과 트로벌류트 곡선의 수식입니다.(m은 θ에 영향을 미치지 않으므로 제거된 수식입니다.) 인벌류트 곡선과 트로벌류트 곡선이 만나는 점의 θi값은 θis가 되고 θt값은 θte가 되므로 비선형 연립방정식을 풀면 됩니다. 비선형 연립방정식 해법에서 소개한 수식을 보면 아래와 같습니다. 두 곡선이 만나는 점은 같은 좌표를 말하며 위와 같이 쓸 수 있습니다. 위 식으로 F행렬을 만듭니다. 위는 야코비안 행렬입니다. 위의 인벌류트 곡선의 수식과 트로벌류트 곡선의 수식을 미분하면 아래와 같습니다. 위 식을 정리하면 아래와 같습니다. F행렬이 0이 될 때까지 위..